6. 物体的位置和旋转
本教程翻译自官方教程Position and Rotation,各位也可以进入本站镜像站点查看
本文目录
位置Position,旋转Rotation和缩放Scaling
Babylon101定位入门级课程,所以在本章只会介绍物体的位置Position, 旋转Rotation 和 缩放Scaling三个设置参数。更多有关改变物体位置、方向的方法请各位移步到延生阅读中去进一步探索。
关于三种方法都需要一个 坐标参照系 ,也就是让一个物体如何改变位置、旋转和缩放的规则。而且为了很好的让大家理解 坐标参照系 ,我们使用了一个不规则形状,称为 实验体 ,用来帮助我们理解位置、旋转和缩放。

实验体的样子,其实就是一个立方体加上圆锥体
坐标参照系
Babylon.js使用了两种 坐标参照系 ,即世界坐标系world和局部坐标系local,世界坐标系可以理解为:全局坐标系。世界坐标系的原点位置任何时候都是(0, 0, 0)不会被改变,而局部坐标系会随着物体位置、旋转、缩放的改变而改变。例如:一个物体的初始位置是(0, 0, 0),它世界坐标系和局部坐标系就都是(0, 0, 0),当这个物体移动到位置(0, 10, 0)的时候,也就是向上移动了10的距离,这个时候它世界坐标系还是(0, 0, 0)和局部坐标系是(0, 10, 0)。
在Playground例子的中,坐标的轴线都有标准的颜色标识,X轴为红色,Y轴为绿色,Z轴为蓝色。
创建物体时,物体的中心就在世界坐标的原点(0, 0, 0)处,其位置的值始终是一个相对于世界坐标原点的值。例如位置(0, 10, 0),就是相对于(0, 0, 0)网上偏离了10个单位。
之前也讲到,局部坐标是随着物体的移动而移动的,并且无论物体的位置、方向、大小如何,局部坐标的原点始终在会处于物体的中心。物体旋转和缩放需要一个支点,一般来说都是位于其局部坐标的原点,简单来说也就是该物体的中心,所以我们看到的效果就是中心缩放和中心旋转。如果想改变支点怎么办?比如地球绕着太阳旋转,支点就肯定不能是自身中心,强大的Babylon肯定是有办法的,那就是通过使用变换节点TransformNode或矩阵Matrix来为物体设置新的支点。
向量Vectors
所有位置,旋转和缩放比例均使用三维矢量分别设置,设置的格式为:BABYLON.Vector3(x,y,z)
实验体The Pilot
在创建一个物体后,默认旋转角度为0,缩放比例为1,所以实验体的位置也显示在世界坐标的原点(0, 0, 0),而且世界坐标轴和局部坐标轴此时是重合在一起的。
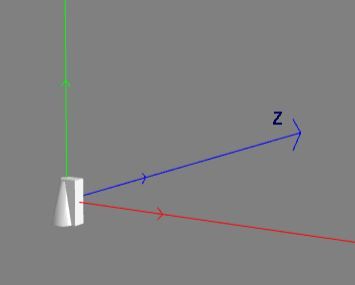
带坐标轴的实验体
位置Position
位置Position参照世界坐标轴来放置实验体,使用的是三维向量vector3 (x, y, z),局部坐标轴随着实验体的移动而移动。
//常规设置
pilot.position = new BABYLON.Vector3(2, 3, 4);
//或者,独立设置
pilot.position.x = 2;
pilot.position.y = 3;
pilot.position.z = 4;
虽然局部坐标轴的位置发生了变化,但是它和世界坐标轴的方向是一致的。
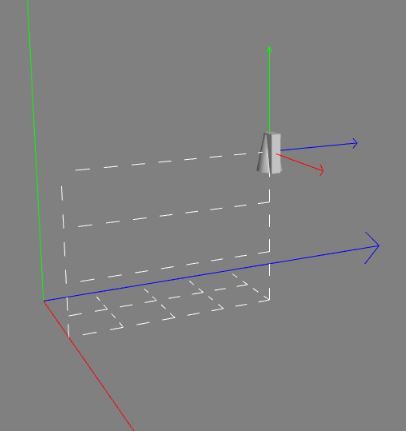
旋转Rotation
真香警告!在3D空间中处理旋转是非常棘手的,首先对一个物体应用多次旋转操作,而应用这些旋转操作的先后顺序可能会导致物体有着完全不同的方向,其次我们还需要知道使用的是世界坐标还是局部坐标,这也是在旋转中影响物体方向的因素之一。把旋转操作应用到3D模型上,这有很多通用准则。想了解Babylon.js中这些相关的准则,请移步欧拉角和四元数。虽然很难,但是功能却很强大!真香
在Babylon.js中对物体设置旋转的代码如下:
//常规设置
pilot.rotation = new BABYLON.Vector3(alpha, beta, gamma);
//或者,独立设置
pilot.rotation.x = alpha; //围绕X轴旋转
pilot.rotation.y = beta; //围绕Y轴旋转
pilot.rotation.z = gamma; //围绕Z轴旋转
以上代码中的alpha, beta, and gamma是以弧度作为单位的,也就是说与我们平时所说的角度不一样,例如360°,有一个换算公式:
1° = π /180 弧度
可能的疑问:上面代码中分别设置了alpha, beta, gamma,针对了X、Y、Z三个轴,而且之前又说了旋转操作的先后顺序和使用的坐标系会影响最终方向,那么你会问了“代码中的旋转操作设置了alpha、beta、gamma,那它们三个分别使用了世界坐标系还是局部坐标系?应用的顺序如何?”
其实对于Babylon.js中旋转,以下两个准则得出的结果都是一样的:
准则1-局部坐标系
对于局部坐标,物体以中心为原点并沿着其局部坐标轴进行旋转,旋转的顺序为Y、X、Z。如果我们按照三个不同方向正对着观察物体的旋转,那么它们的旋转方向都是逆时针。
下图中按照顺序展示了执行旋转操作后实验体的方位,图1.初始状态、 图2. 绕着局部坐标系Y轴旋转π/2弧度、图3. 围绕局部坐标系X轴旋转π/2弧度、图4. 围绕局部坐标系Z轴旋转了π/2弧度。
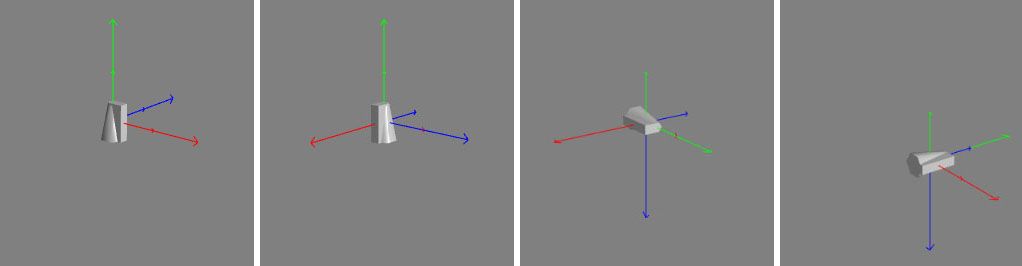
图中较小的轴表示世界轴的方向,就是线中间有个小点,各位要仔细看。
准则2-世界坐标系
又称为全局坐标系,与准则1的局部坐标相比,按照世界坐标对物体进行旋转:旋转中心点没有变,但是旋转轴线变了。
对于世界坐标,物体以中心为原点保持和之前一样,沿着与世界坐标轴进行旋转,旋转的顺序为Z、X、Y。如果我们按照三个不同方向正对着观察物体的旋转,那么它们的旋转方向都是逆时针。
下图中按照顺序展示了执行旋转操作后实验体的方位,图1.初始状态、 图2. 绕着世界坐标系Z轴旋转π/2弧度、图3. 围绕局部坐标系X轴旋转π/2弧度、图4. 围绕局部坐标系Y轴旋转了π/2弧度
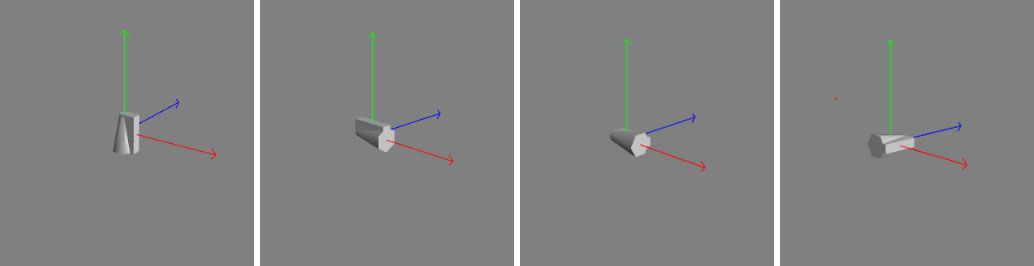
总结
我们可以看到,无论以何种方式进行旋转,最后的结果始终是相同的。 以下代码产生的结果都相同:
pilot.rotation = new BABYLON.Vector3(alpha, beta, gamma);
pilot.rotation.x = alpha;
pilot.rotation.y = beta;
pilot.rotation.z = gamma;
pilot.rotation.z = gamma;
pilot.rotation.x = alpha;
pilot.rotation.y = beta;
pilot.rotation.y = beta;
pilot.rotation.z = gamma;
pilot.rotation.x = alpha;
一系列的旋转操作
假如你想要进行一系列的旋转操作,例如先围绕x轴旋转,再围绕y轴旋转,最后围绕z轴旋转,这应该怎么办呢?
其实在babylon这很简单,使用rotate方法,可以自定义是作用于世界坐标系还是局部坐标系。使用addRotation方法,仅针对局部坐标系。
我们详细介绍下addRotation方法,它可以进行链式调用,接受3个弧度参数值,分别对应X、Y、Z三个坐标轴。用法如下所示:
mesh.addRotation(Math.PI/2, 0, 0).addRotation(0, Math.PI/2, 0).addRotation(0, 0, Math.PI/2);
以下的图例,用addRotation展示了实现 Playground 物体旋转实例 中的旋转案例,还是以实验体作为参照,图1、初始状态,无旋转;图2、绕局部X轴旋转π/ 2;图3、再绕着局部Y轴旋转π/ 2;图4、最后绕着局部Z轴旋转π/ 2。
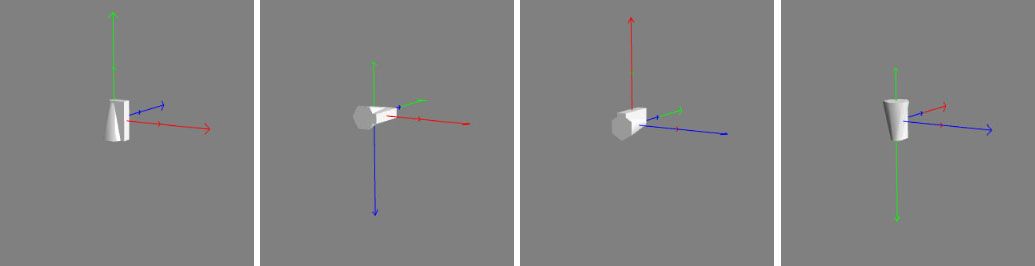
图中较小的轴表示世界轴的方向,就是线中间有个小点,各位要仔细看。
一般来说,mesh.addRotation(alpha,beta,gamma)只对其中1个参数设置弧度制,剩下2个设为0,要不然行为会很怪异(也不知道官方怎么考虑的),其中alpha是围绕局部x轴的旋转,beta是围绕局部y轴的旋转,gamma是围绕局部z轴的旋转。
RotationQuaternions方法介绍
还有一种旋转方法,那就是用rotationQuaternions方法直接操作四元数 Quaternions ,这个方法很抽象、很难,但好处就是接近底层,让你随意发挥。但是需要注意,这种方法和之前介绍的方法是不能同时使用到一个物体上的,具体请看这里。
缩放Scaling
缩放相对来说比较简单,不存在需要处理世界坐标的问题,我们只需要按照如下方法来沿着局部坐标X、Y、Z轴进行旋转即可。
//常规设置
mesh.scaling = new BABYLON.Vector3(scale_x, scale_y, scale_z);
//或者,独立设置
mesh.scaling.x = 5;
mesh.scaling.y = 5;
mesh.scaling.z = 5;
下图显示了围绕z轴旋转并沿局部y轴缩放的一个立方体。
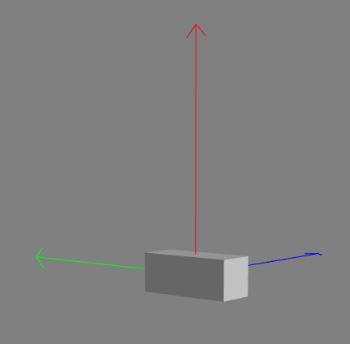
X轴为红色,Y轴为绿色,Z轴为蓝色。
下一步
现在你应该知道如何在场景中创建一个物体,然后移动、旋转、缩放它了,但是你会发现创建的物体都长一个样,为了让他们变得更漂亮点,请阅读下一章材质materials-美化你的物体。
延伸阅读
功能
贡献者
参与贡献? 联系alexads@foxmail.com